Articles de muscate

Un exercice pour mettre en application ce que vous avez appris sur l'équation de la tangente en un point d'une courbe:

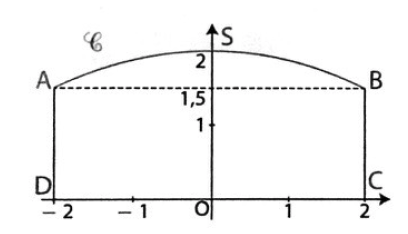
Un fabriquant doit réaliser un portail en bois plein sur mesure selon le schéma ci dessous.

L'unité du repère représente 1 mètre.

L'arc (AB) est  une partie de la courbe représentative d'une fonction f définie sur [-2;2] par f(x)=ax²+bx+c avec a,b,c nombres réels et a non nul.

1. a) La tangente à la courbe au point d'abscisse 0 est parallèle à l'axe des abscisses.

Justifier que f'(0)=0 et en déduire la valeur de b.

b) À l'aide des informations f(0)=2 et f(2)=1,5, déterminer les valeurs de a et c.

En déduire que pour tout x de l'intervalle [-2;2]:

f(x)=-0,125x²+2

2. a) Vérifier que f est une fonction paire.

b) Interpréter cette propriété.

3. Pour découper les vantaux du portail, le fabricant découpe des planches. Il a le choix entre deux formes de planches prédécoupées: soit un carré OCES, soit un trapèze OCHG comme dans les schémas ci-dessous.

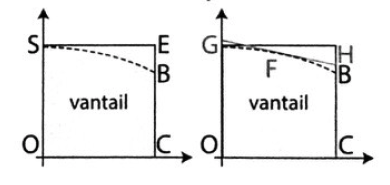Dans la deuxième méthode, la droite (GH) est la tangente à la courbe au point F d'abscisse 1.

Quelle est la forme la plus économique?

Voir la solution en vidéo:

Un exercice sur la loi des probabilités totales : ( pour terminale et première):

On lance un dé non truqué à 6 faces numérotées de 1 à 6 et on note le résultat obtenu.

Si le résultat est pair, on lance un dé non truqué à 20 faces numérotées de 1 à 20.

Si le résultat est impair, on lance un dé non truqué à huit faces numérotées de 1 à 8.

Quelle est la probabilité pour que le résultat du deuxième dé soit un nombre premier?

Essayez de résoudre ce problème avec ce que vous avez appris sur le chapitre des probas!

Un jeu oppose un présentateur à un candidat. Le candidat est placé devant trois portes fermées, notées 1,2 et 3. Derrière l'une d'elles se trouve une voiture et derrière les deux autres, une boîte de bonbons. Le jeu se déroule en deux étapes. Utiliser les différentes informations pour déterminer si, à la suite de la première étape, le candidat a intérêt à changer son choix ou non.

Un exercice de recherche qui mélange probas et étude de fonction!

Un pion est placé sur la case centrale d'une ligne de 5 cases. À chaque étape, on déplace le pion vers la droite avec une probabilité de (1/n), où n est un entier naturel non nul, ou vers la gauche.
Lauriane affirme: "Plus n augmente, plus la probabilité que le pion soit au centre après deux déplacements diminue."
Démontrer ou infirmer la conjecture de Lauriane.

Un exercice qui mélange calcul algébrique et géométrie. Exploitez vos connaissances!

Une piscine de 25m de long est à fond plat sur 12,5m et à fond incliné sur 12,5m également. Les propriétaires souhaitent remplir cette piscine.

Utiliser les différentes informations pour déterminer la hauteur d'eau, en m, maximum dans la piscine.

Arrondir au dixième.

Pensez à utiliser le théorème de Thales et les équations du second degré.

Apprendre à tracer la section d'un cube par un plan . 

Apprendre à établir la forme canonique d'un polynôme du second degré à partir de sa forme développée .

Trouver la forme canonique de:

1)  f(x)= 4x² -3x +5

2)  g(x)=5x²+4x-3

Voir la vidéo explicative: NB: petite erreur de signe à 7:11 ( + 2 x a x b au lieu de - 2 x a x b)

Télécharger le pdf de la correction:

comple-tion-du-carre--1.pdf (146.01 Ko)

Voici un exercice de réflexion sur les suites; il s'agit de trouver la formule explicite d'une suite qui n'est ni arithmétique ni géométrique, à partir de sa formule de récurrence.

Il faut aller chercher parmi ses connaissances du cours et faire intervenir son intuition pour trouver le chemin vers la solution.

Soit la suite (U_n) définie par U₀=2 et pour tout entier naturel n ≥ 1 par: U_n = U_n-1 + 4n+1 

Exprimer U_n en fonction de n

Voir la solution en vidéo:

Télécharger le pdf de la correction:

suites-prise-d-initiative-1.pdf (164.58 Ko)