dérivées tangente équation maths première spécialité

Un exercice pour mettre en application ce que vous avez appris sur l'équation de la tangente en un point d'une courbe:

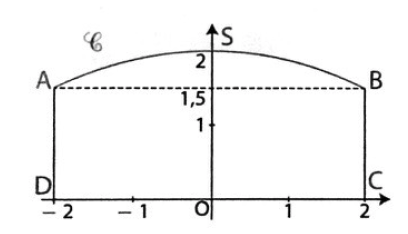
Un fabriquant doit réaliser un portail en bois plein sur mesure selon le schéma ci dessous.

L'unité du repère représente 1 mètre.

L'arc (AB) est  une partie de la courbe représentative d'une fonction f définie sur [-2;2] par f(x)=ax²+bx+c avec a,b,c nombres réels et a non nul.

1. a) La tangente à la courbe au point d'abscisse 0 est parallèle à l'axe des abscisses.

Justifier que f'(0)=0 et en déduire la valeur de b.

b) À l'aide des informations f(0)=2 et f(2)=1,5, déterminer les valeurs de a et c.

En déduire que pour tout x de l'intervalle [-2;2]:

f(x)=-0,125x²+2

2. a) Vérifier que f est une fonction paire.

b) Interpréter cette propriété.

3. Pour découper les vantaux du portail, le fabricant découpe des planches. Il a le choix entre deux formes de planches prédécoupées: soit un carré OCES, soit un trapèze OCHG comme dans les schémas ci-dessous.

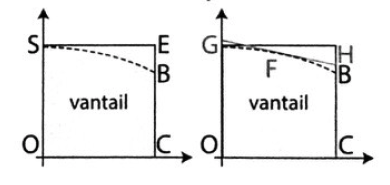Dans la deuxième méthode, la droite (GH) est la tangente à la courbe au point F d'abscisse 1.

Quelle est la forme la plus économique?

Voir la solution en vidéo: